Two Generals' Problem

在分布式系统中最广为人知并且最突出的关于共识的描述是对于 Two Generals' Problem 两将军问题的实验性思考。

这个思考展示了在可能产生故障的连接上进行的异步的通信，是不可能实现共识的。尽管 TCP 展示了 Perfect link 完美连接的属性，但需要记住一个非常重要的点，连接是完美的并不保证完美的送达。他也没有保证参与者们在整个过程都能够存活，他所关注的只有信息的传输，

假设有两支军队由两个将军统领，并准备去攻打一个城市。军队分别驻扎在城市的两边并且只有两边同时进行围攻才能战胜。

将军们则是使用发送消息的方式来进行通信，并且已经制定好了攻击的计划。现在他们剩下要做的是是否要去执行这个计划。这个问题有一些变种是其中一个将军具有更高的级别，但需要确保去协调这次攻击；或者是将军们需要先对具体的时间达成共识。这些细节并没有有改变这个问题的定义：将军们需要达成某种共识。

军队的将军需要的是达成的共识是要么一起去执行这次进攻，要么都不进攻。将军 A 发送了消息 MSG(N)，表明如果其他人也同意的话，这次进攻会在一个指定的时间开始。

在 A 派出了这个信使之后没办法确认信使是否已经传达消息：因为信使可能被俘虏了导致没法送达消息。在将军 B 接收到这个消息后，他需要发送出他的确认消息 ACK(MSG(N))。Figure 8-4 展示了消息发送出去然后收到另一方的确认的情况。

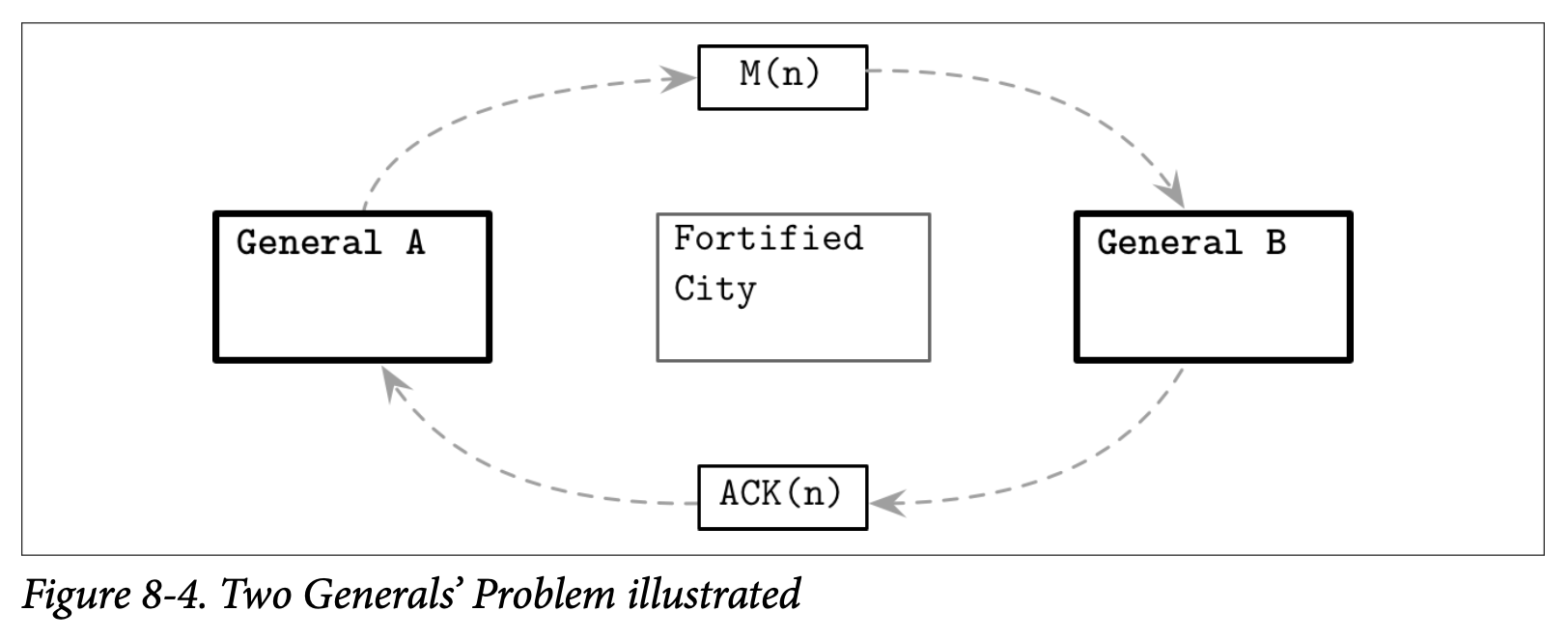
而负责传递确认消息的信使也可能会因为被俘虏导致消息传递失败。同样的 B 也没有任何办法能够知道信使是否能够将确认的消息送达。

为了确认这点，B 需要等待 ACK(ACK(MSG(N)))，第二个用来确认 A 已经收到确认消息的确认消息。

不管将军们相互发送了多少次确认的消息，为了能够安全的处理这次进攻，他们最后总会剩一个 ACK 消息是需要确认的。将军们必然会怀疑最后的这个确认消息是否安全的送达。

我们会发现没有做任何时间上的假设：两个将军的通信是完全异步的。在这里并没有设置将军需要作出回复的时间上限。