Binary Search Trees
二叉搜索树 (BST) 是有序的内存数据结构,被用来提供高效的基于键值对的查找。BST 包含了许多的节点,每个树的节点都呈现为一个 Key 及跟该 Key 相关联的数据,每个节点有两个子节点 (因此取名二叉)。BST 从一个单独的名为 root 的节点开始,并且一棵树只允许有一个 root 节点。Figure 2-1 中我们展示了个二叉搜索树的例子
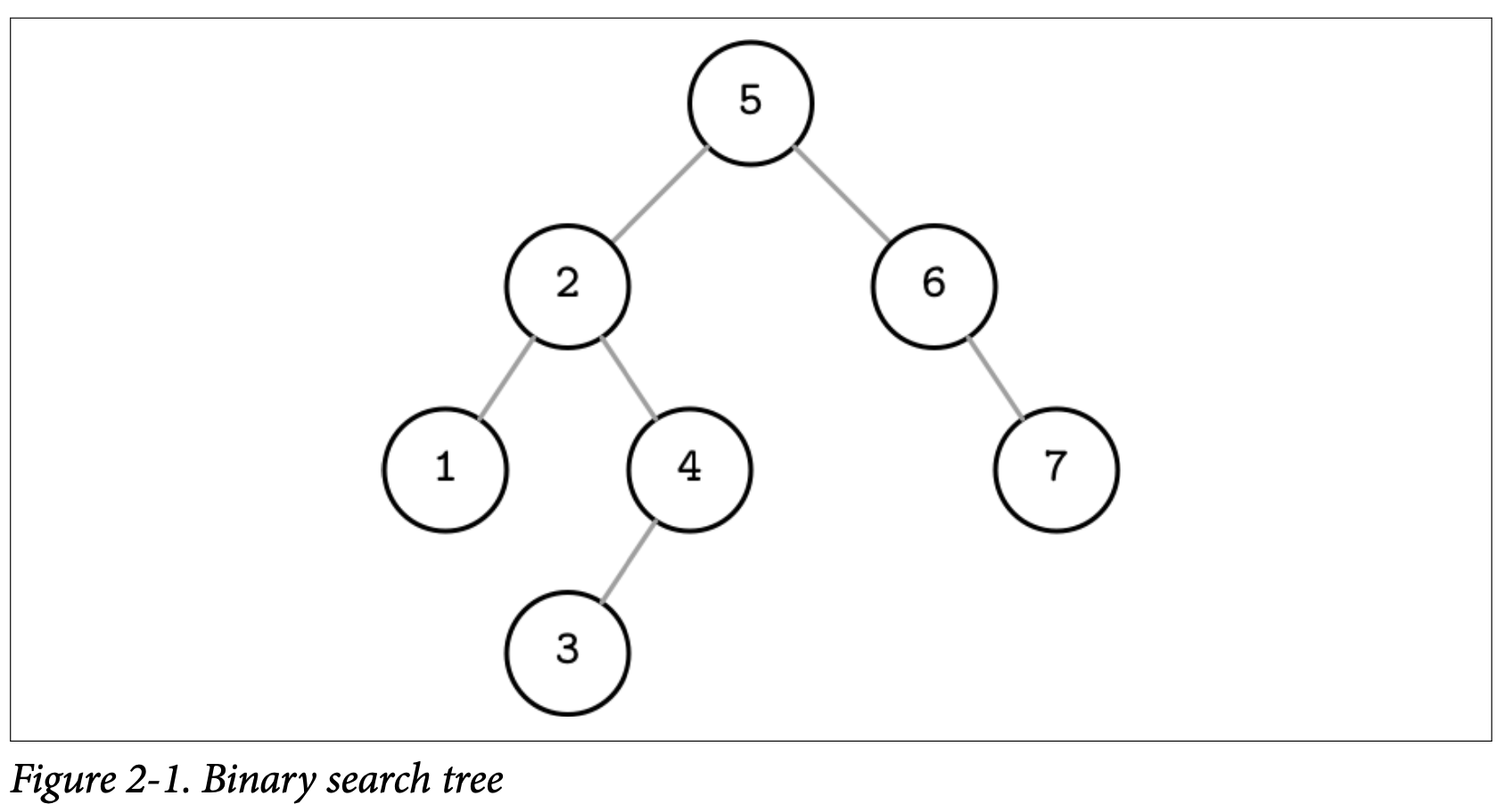
每个节点将搜索空间分割为左子树 subtrees 跟右子树,正如 Figure 2-2 展示的,一个节点的 Key 会大于其左子树的所有节点,并且会小于其右子树的所有节点。
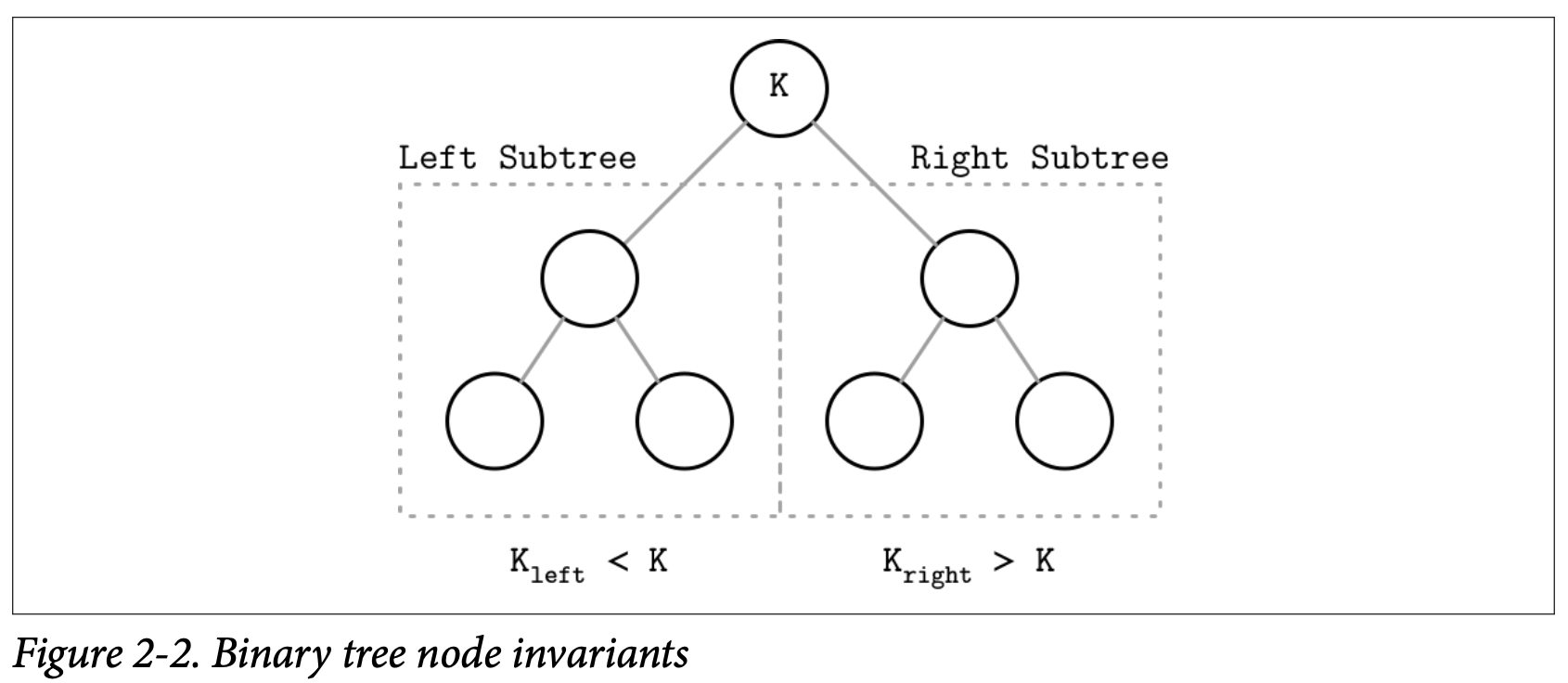
从 root 开始沿着左子树一直遍历到最左的叶子节点 (叶子意味着他不具有子节点) 就能定位到树中最小的 Key 以及其关联的数据。同样的,沿着右子树一直遍历到最右的叶子节点能够定位到树中最大的 Key 及其关联的数据。关联的数据允许存储在树中的任意节点中,然后查找会从 root 节点开始,但可能会在非叶子节点就被中断或返回,比如已经在较高的层级中找到了对应的 Key。
Tree Balancing
插入的操作并不会遵循哪种指定的方式,元素的插入可能会导致树失去平衡 (比如其中一个分支比其他的分支要长)。在 Figure 2-3 中展示了最严重的场景,其中展示了一颗看起来更像是链表的病态的树,作为一个设计目标是对数复杂度的树 (如 Figure 2-3 ),最后演变成了线性复杂度。
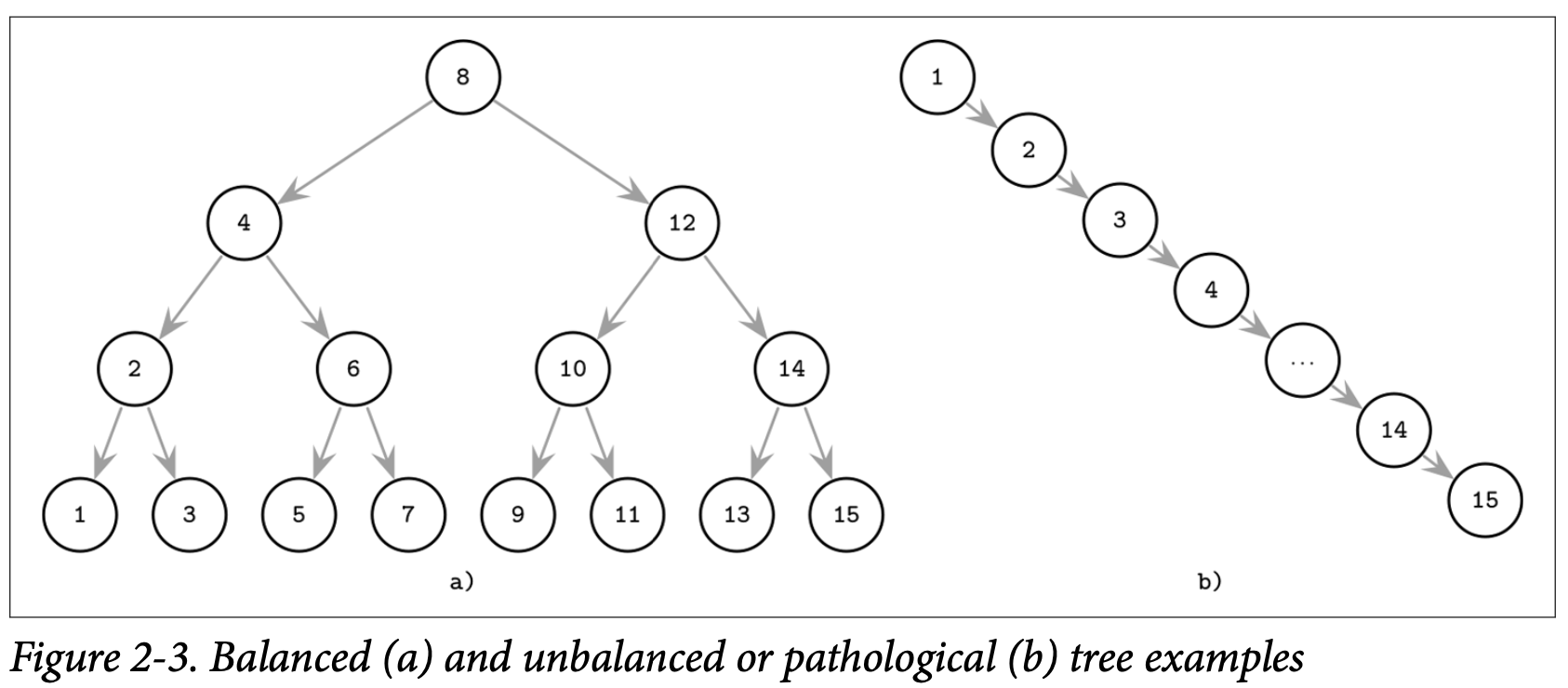
这个例子可能将问题描述的略微极端了,但他说明了为什么树需要平衡性: 尽管不是所有的节点最后都会往一边倾斜,但毫无疑问的是这种情形会显著的降低查询效率。
一个平衡的树的高度是被定义为了 Log2N,N 是指树中所有节点的总数,并且左右两颗子树的高度只差不会超过一。在失去平衡时,我们会失去二叉搜索树的结构给我们的性能优势,并且插入跟删除操作也会影响树的形状 (平衡)。
在一颗平衡的树中,在平均情况下每次进入左子树或右子树都能够减少一半的查找空间,所以查找的复杂度为 O(log2 N)。如果树是失衡的,最差的情况下复杂度会增长为 O(N),因为我们最终可能会遇到树的所有节点都在同一侧的情况。
为了不产生在添加新元素后其中一侧分支越来越长,另一侧却还是空的情况 (如 Figure 2-3 (b)),让树继续保持平衡。可以通过重新组织树的节点来降低树的高度,并让两侧分支的差距保持一定的边界。后
其中一种保持树平衡的方法是在添加或删除树的节点对其进行翻转。如果插入的操作导致让当前分支失衡 (分支里两个连续的节点只有一个子节点),我们就可以 rorate 旋转中间的节点,如 Figure 2-4 中展示的,对 node(3) 进行旋转,我们称它为 pivot 节点,旋转后将它提高几个层级,并且将它的父节点设为右子节点。
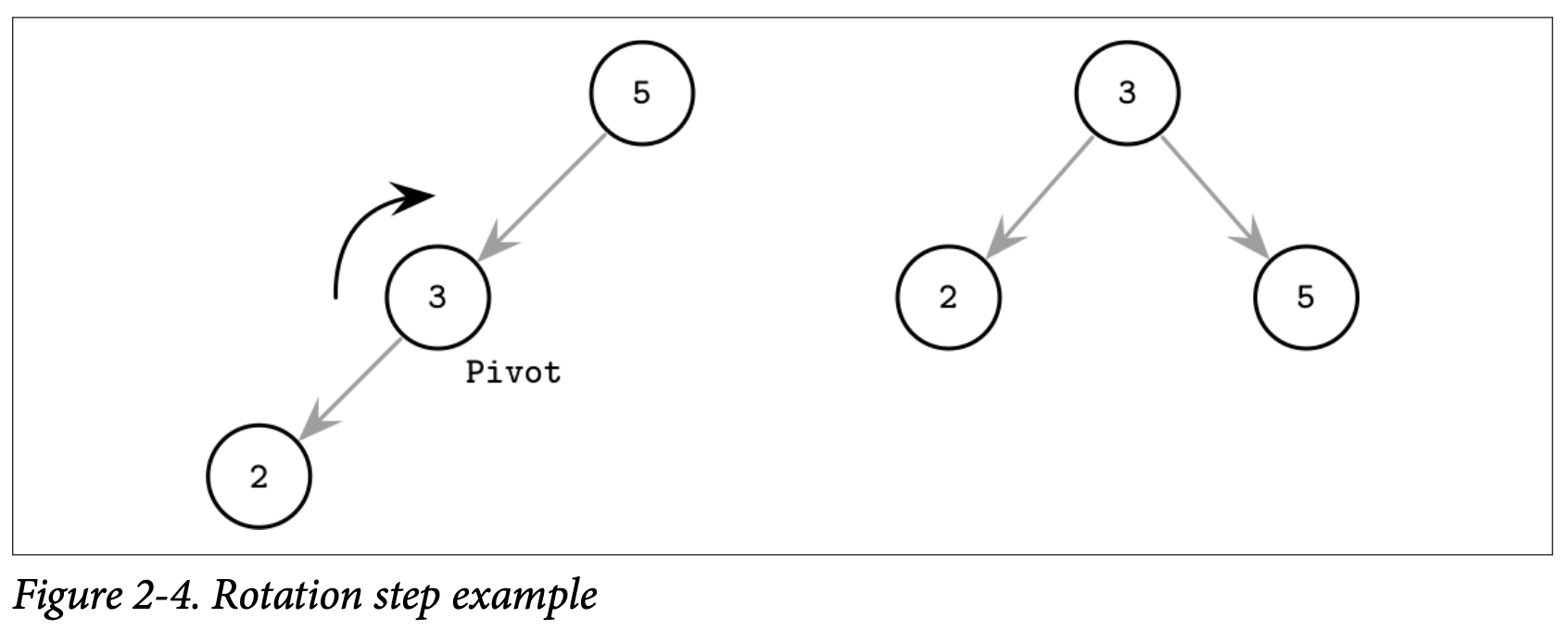
Trees for Disk-Based Storage
如前面提到的,失衡的树有着糟糕的 O(N) 的复杂度。平衡树给我们的平均复杂度应该是 O(log2 N)。在这个时候下,由于扇出量很低 (扇出量是我们允许的节点所能拥有的最大子节点数),我们需要频繁的去维持树的平衡,旋转节点,并更新对应的指针等信息。高昂的管理成本让 BST 作为基于磁盘的数据结构成了不现实的选择。
如果我们希望在磁盘中管理 BST,需要面对几个问题。其中一个是局部性:数据是以随机的顺序添加的,没办法保证新增的节点会写到其父节点附近,这意味着节点的子节点可能会在多个磁盘页中保存。我们可以通过调整树的布局跟使用基于页的二叉树来改善这种情况。
另外一个问题跟子节点也是紧密相关的,就是树的高度。因为二叉树的扇出量只有二,因此高度是树节点总数的以二为底的对数,因此我们需要花费 O(log2 N) 次寻址来定位需要查找的元素,并导致相同次数的磁盘数据传输。2-3-Tree 跟其他扇出量低的树都具有相同的限制:他们可以高效的在内存中使用,但较少的节点数意味着将他们应用到外部存储器时变得不现实。
一个拙劣的基于磁盘的 BST 实现需要许多的磁盘寻址来做比较,因为他没有建立起局部性的概念。这让我们踏上了寻找具有这种特性的数据结构的路。
考虑到这些因素,一个能够适配磁盘的树的实现需要满足下面两个特性:
- Hight fanout 高扇出能够提高邻接节点的局部性
- Low height 低高度能够减少查找过程所需的次数
扇出跟高度有着一个相反的关系:更高的扇出量意味着更低的高度。如果扇出很高,每个节点能够持有的子节点数会更多,这减少了整体的节点数,因此也会产生更低的高度。